let the three heights of ⊿abc be ad, be, and cf, among which d, e, and f are the vertical feet, the vertical center is h, and the opposite sides of angles a, b, and c are a, b, and c respectively.

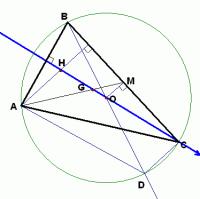
1. the perpendicular center of an acute-angled triangle is inside the triangle; the perpendicular center of a right-angled triangle is on the vertex of the right angle; and the perpendicular center of an obtuse-angled triangle is outside the triangle.

2. the perpendicular center of a triangle is the incenter of its perpendicular triangle; in other words, the incenter of a triangle is the perpendicular center of its paracenter triangle; 3. the symmetry points of the perpendicular center h with respect to the three sides are all on the circumcircle of △abc.

4. in △abc, there are six groups of four points cocirculating, and there are three groups (four in each group) of similar right triangles, and ah·hd=bh·he=ch·hf.

5. any point among the four points h, a, b, and c is the orthocenter of the triangle with the remaining three points as vertices (and such four points are called a-orthocenter group).

6. the circumscribed circles of △abc, △abh, △bch and △ach are equal circles.

7. in a non-right triangle, if the straight line passing through h intersects the straight lines ab and ac at p and q respectively, then ab/ap·tanb+ac/aq·tanc=tana+tanb+tanc.

8. the distance from any vertex of a triangle to the vertical center is equal to twice the distance from the circumcenter to the opposite side.

9. assume o and h are the circumcenter and orthocenter of △abc respectively, then ∠bao=∠hac, ∠abh=∠obc, ∠bco=∠hca.

10. the sum of the distances from the orthocenter of an acute triangle to its three vertices is equal to twice the sum of the radii of its inscribed and circumscribed circles.

11. the perpendicular center of an acute triangle is the incenter of the perpendicular triangle; among the inscribed triangles of the acute triangle (the vertices are on the sides of the original triangle), the perimeter of the perpendicular triangle is the shortest.

12. simson's theorem (simson's line): a necessary and sufficient condition for the collinearity of the vertical legs of a perpendicular drawn from a point to the three sides of a triangle is that the point falls on the circumcircle of the triangle.

13. suppose there is a point p within the acute angle ⊿abc, then the necessary and sufficient condition for p to be the vertical center is pb*pc*bc+pb*pa*ab+pa*pc*ac=ab*bc*ca.